terminology
-
polygon = list of vertexes used to represent a
closed polygon
-
graph= list of links, represents the segments
of the original polygons.
-
graphlist = list of graphs
-
link = connection between two nodes (represents
one segment of the original polygon)
-
node = connection between several links, has a
(x,y) position
graphs
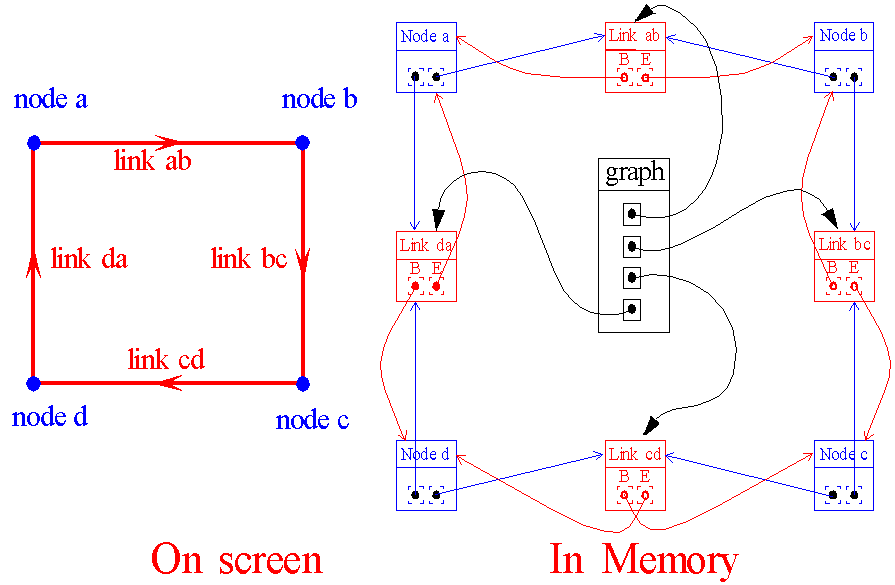
The boolean operation uses an internal data structure that is based on
graphs. The original polygons are first converted into graphs, each polygon
becomes one graph. A graph is in principal a list of segments/links,
where each link has two pointers. One pointer to the beginnode of the segment
and one to the endnode. Several links can share the same node. At first
each node in the graph will be referenced by two links, the reason is that
the original polygon is always a closed shape. All the links in a graph
get a unique number to tell that they belong to a certain polygon.
When intersections between graphs have been calculated at the intersection
points, new nodes are created that can have many links
pointing to it, but at least 4 links. In Graph
structure. the memory structure of the graph that represent a polygon
containing 4 vertexes is
shown. In Intersection of graph
links. is shown what happens when an intersection point is found. At
the intersection point of the two
intersecting links, a new node is inserted and the original links are
split into two parts.
For the intersection process the seperate graphs are merged into one
big graph. After intersection of several graphs, the original polygons
can still
be distinguished by following the unique number of a specific link.
When all intersections are known, a flag is set for the right and left
side of each link to tell if it belongs to groupA or groupB enclosed areas.
Based on this information the proper result for a given boolean operation
can be extracted.
Graph structure
Intersection of graph
links


